A user guide to Azure ML Cheat Sheet. A cheat sheet for common use cases with AML. Get 80% of what you need in 20% of the documentation. 1 cubic meter is equal to 58919 oz, or 1000000 ml. Note that rounding errors may occur, so always check the results. Use this page to learn how to convert between ounces and milliliters. Type in your own numbers in the form to convert the units! ›› Quick conversion chart of oz to ml. 1 oz to ml = 29.57353 ml. 2 oz to ml = 59.14706 ml. CS312 SML / NJ Cheat Sheet: unit 3: int 3.0: real #'a': char 'xyz': string false: bool 3.
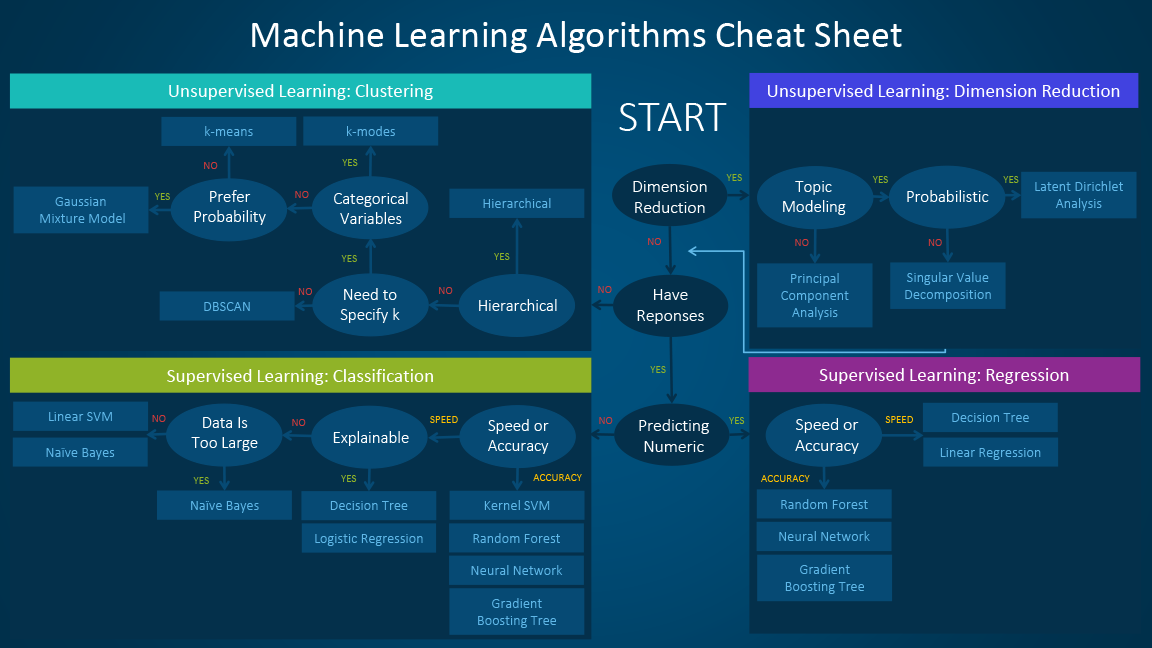
A common question is “Which machine learning algorithm should I use?” The algorithm you select depends primarily on two different aspects of your data science scenario:
What you want to do with your data? Specifically, what is the business question you want to answer by learning from your past data?
What are the requirements of your data science scenario? Specifically, what is the accuracy, training time, linearity, number of parameters, and number of features your solution supports?
Business scenarios and the Machine Learning Algorithm Cheat Sheet
The Azure Machine Learning Algorithm Cheat Sheet helps you with the first consideration: What you want to do with your data? On the Machine Learning Algorithm Cheat Sheet, look for task you want to do, and then find a Azure Machine Learning designer algorithm for the predictive analytics solution.
Machine Learning designer provides a comprehensive portfolio of algorithms, such as Multiclass Decision Forest, Recommendation systems, Neural Network Regression, Multiclass Neural Network, and K-Means Clustering. Each algorithm is designed to address a different type of machine learning problem. See the Machine Learning designer algorithm and module reference for a complete list along with documentation about how each algorithm works and how to tune parameters to optimize the algorithm.
Note
To download the machine learning algorithm cheat sheet, go to Azure Machine learning algorithm cheat sheet.
Along with guidance in the Azure Machine Learning Algorithm Cheat Sheet, keep in mind other requirements when choosing a machine learning algorithm for your solution. Following are additional factors to consider, such as the accuracy, training time, linearity, number of parameters and number of features.
Comparison of machine learning algorithms
Some learning algorithms make particular assumptions about the structure of the data or the desired results. If you can find one that fits your needs, it can give you more useful results, more accurate predictions, or faster training times.
The following table summarizes some of the most important characteristics of algorithms from the classification, regression, and clustering families:
| Algorithm | Accuracy | Training time | Linearity | Parameters | Notes |
|---|---|---|---|---|---|
| Classification family | |||||
| Two-Class logistic regression | Good | Fast | Yes | 4 | |
| Two-class decision forest | Excellent | Moderate | No | 5 | Shows slower scoring times. Suggest not working with One-vs-All Multiclass, because of slower scoring times caused by tread locking in accumulating tree predictions |
| Two-class boosted decision tree | Excellent | Moderate | No | 6 | Large memory footprint |
| Two-class neural network | Good | Moderate | No | 8 | |
| Two-class averaged perceptron | Good | Moderate | Yes | 4 | |
| Two-class support vector machine | Good | Fast | Yes | 5 | Good for large feature sets |
| Multiclass logistic regression | Good | Fast | Yes | 4 | |
| Multiclass decision forest | Excellent | Moderate | No | 5 | Shows slower scoring times |
| Multiclass boosted decision tree | Excellent | Moderate | No | 6 | Tends to improve accuracy with some small risk of less coverage |
| Multiclass neural network | Good | Moderate | No | 8 | |
| One-vs-all multiclass | - | - | - | - | See properties of the two-class method selected |
| Regression family | |||||
| Linear regression | Good | Fast | Yes | 4 | |
| Decision forest regression | Excellent | Moderate | No | 5 | |
| Boosted decision tree regression | Excellent | Moderate | No | 6 | Large memory footprint |
| Neural network regression | Good | Moderate | No | 8 | |
| Clustering family | |||||
| K-means clustering | Excellent | Moderate | Yes | 8 | A clustering algorithm |
Requirements for a data science scenario
Once you know what you want to do with your data, you need to determine additional requirements for your solution.
Make choices and possibly trade-offs for the following requirements:
- Accuracy
- Training time
- Linearity
- Number of parameters
- Number of features
Accuracy
Accuracy in machine learning measures the effectiveness of a model as the proportion of true results to total cases. In Machine Learning designer, the Evaluate Model module computes a set of industry-standard evaluation metrics. You can use this module to measure the accuracy of a trained model.
Getting the most accurate answer possible isn’t always necessary. Sometimes an approximation is adequate, depending on what you want to use it for. If that is the case, you may be able to cut your processing time dramatically by sticking with more approximate methods. Approximate methods also naturally tend to avoid overfitting.
There are three ways to use the Evaluate Model module:
Ml Cheat Sheet Github
- Generate scores over your training data in order to evaluate the model
- Generate scores on the model, but compare those scores to scores on a reserved testing set
- Compare scores for two different but related models, using the same set of data
For a complete list of metrics and approaches you can use to evaluate the accuracy of machine learning models, see Evaluate Model module.
Training time
In supervised learning, training means using historical data to build a machine learning model that minimizes errors. The number of minutes or hours necessary to train a model varies a great deal between algorithms. Training time is often closely tied to accuracy; one typically accompanies the other.
In addition, some algorithms are more sensitive to the number of data points than others. You might choose a specific algorithm because you have a time limitation, especially when the data set is large.
In Machine Learning designer, creating and using a machine learning model is typically a three-step process:
Configure a model, by choosing a particular type of algorithm, and then defining its parameters or hyperparameters.
Provide a dataset that is labeled and has data compatible with the algorithm. Connect both the data and the model to Train Model module.
After training is completed, use the trained model with one of the scoring modules to make predictions on new data.
Linearity
Linearity in statistics and machine learning means that there is a linear relationship between a variable and a constant in your dataset. For example, linear classification algorithms assume that classes can be separated by a straight line (or its higher-dimensional analog).
Lots of machine learning algorithms make use of linearity. In Azure Machine Learning designer, they include:
Linear regression algorithms assume that data trends follow a straight line. This assumption isn't bad for some problems, but for others it reduces accuracy. Despite their drawbacks, linear algorithms are popular as a first strategy. They tend to be algorithmically simple and fast to train.
Nonlinear class boundary: Relying on a linear classificationalgorithm would result in low accuracy.
Data with a nonlinear trend: Using a linear regression method wouldgenerate much larger errors than necessary.
Number of parameters
Parameters are the knobs a data scientist gets to turn when setting up an algorithm. They are numbers that affect the algorithm’s behavior, such as error tolerance or number of iterations, or options between variants of how the algorithm behaves. The training time and accuracy of the algorithm can sometimes be sensitive to getting just the right settings. Typically, algorithms with large numbers of parameters require the most trial and error to find a good combination.
Alternatively, there is the Tune Model Hyperparameters module in Machine Learning designer: The goal of this module is to determine the optimum hyperparameters for a machine learning model. The module builds and tests multiple models by using different combinations of settings. It compares metrics over all models to get the combinations of settings.
While this is a great way to make sure you’ve spanned the parameter space, the time required to train a model increases exponentially with the number of parameters. The upside is that having many parameters typically indicates that an algorithm has greater flexibility. It can often achieve very good accuracy, provided you can find the right combination of parameter settings.
Number of features
In machine learning, a feature is a quantifiable variable of the phenomenon you are trying to analyze. For certain types of data, the number of features can be very large compared to the number of data points. This is often the case with genetics or textual data.
A large number of features can bog down some learning algorithms, making training time unfeasibly long. Support vector machines are particularly well suited to scenarios with a high number of features. For this reason, they have been used in many applications from information retrieval to text and image classification. Support vector machines can be used for both classification and regression tasks.
Feature selection refers to the process of applying statistical tests to inputs, given a specified output. The goal is to determine which columns are more predictive of the output. The Filter Based Feature Selection module in Machine Learning designer provides multiple feature selection algorithms to choose from. The module includes correlation methods such as Pearson correlation and chi-squared values.
You can also use the Permutation Feature Importance module to compute a set of feature importance scores for your dataset. You can then leverage these scores to help you determine the best features to use in a model.
Next steps
- For descriptions of all the machine learning algorithms available in Azure Machine Learning designer, see Machine Learning designer algorithm and module reference
- To explore the relationship between deep learning, machine learning, and AI, see Deep Learning vs. Machine Learning
By Afshine Amidi and Shervine Amidi
Classification metrics
In a context of a binary classification, here are the main metrics that are important to track in order to assess the performance of the model.
Confusion matrix The confusion matrix is used to have a more complete picture when assessing the performance of a model. It is defined as follows:
| Predicted class | |||
| + | - | ||
| Actual class | + | TP True Positives | FN False Negatives Type II error |
| - | FP False Positives Type I error | TN True Negatives | |
Main metrics The following metrics are commonly used to assess the performance of classification models:
| Metric | Formula | Interpretation |
| Accuracy | $displaystylefrac{textrm{TP}+textrm{TN}}{textrm{TP}+textrm{TN}+textrm{FP}+textrm{FN}}$ | Overall performance of model |
| Precision | $displaystylefrac{textrm{TP}}{textrm{TP}+textrm{FP}}$ | How accurate the positive predictions are |
| Recall Sensitivity | $displaystylefrac{textrm{TP}}{textrm{TP}+textrm{FN}}$ | Coverage of actual positive sample |
| Specificity | $displaystylefrac{textrm{TN}}{textrm{TN}+textrm{FP}}$ | Coverage of actual negative sample |
| F1 score | $displaystylefrac{2textrm{TP}}{2textrm{TP}+textrm{FP}+textrm{FN}}$ | Hybrid metric useful for unbalanced classes |
ROC The receiver operating curve, also noted ROC, is the plot of TPR versus FPR by varying the threshold. These metrics are are summed up in the table below:
| Metric | Formula | Equivalent |
| True Positive Rate TPR | $displaystylefrac{textrm{TP}}{textrm{TP}+textrm{FN}}$ | Recall, sensitivity |
| False Positive Rate FPR | $displaystylefrac{textrm{FP}}{textrm{TN}+textrm{FP}}$ | 1-specificity |

Conversion Cheat Sheet
AUC The area under the receiving operating curve, also noted AUC or AUROC, is the area below the ROC as shown in the following figure:
Regression metrics
Basic metrics Given a regression model $f$, the following metrics are commonly used to assess the performance of the model:
| Total sum of squares | Explained sum of squares | Residual sum of squares |
| $displaystyletextrm{SS}_{textrm{tot}}=sum_{i=1}^m(y_i-overline{y})^2$ | $displaystyletextrm{SS}_{textrm{reg}}=sum_{i=1}^m(f(x_i)-overline{y})^2$ | $displaystyletextrm{SS}_{textrm{res}}=sum_{i=1}^m(y_i-f(x_i))^2$ |
Coefficient of determination The coefficient of determination, often noted $R^2$ or $r^2$, provides a measure of how well the observed outcomes are replicated by the model and is defined as follows:
Ml Cheat Sheet
[boxed{R^2=1-frac{textrm{SS}_textrm{res}}{textrm{SS}_textrm{tot}}}]Main metrics The following metrics are commonly used to assess the performance of regression models, by taking into account the number of variables $n$ that they take into consideration:
| Mallow's Cp | AIC | BIC | Adjusted $R^2$ |
| $displaystylefrac{textrm{SS}_{textrm{res}}+2(n+1)widehat{sigma}^2}{m}$ | $displaystyle2Big[(n+2)-log(L)Big]$ | $displaystylelog(m)(n+2)-2log(L)$ | $displaystyle1-frac{(1-R^2)(m-1)}{m-n-1}$ |
where $L$ is the likelihood and $widehat{sigma}^2$ is an estimate of the variance associated with each response.
Model selection
Vocabulary When selecting a model, we distinguish 3 different parts of the data that we have as follows:
| Training set | Validation set | Testing set |
| • Model is trained • Usually 80% of the dataset | • Model is assessed • Usually 20% of the dataset • Also called hold-out or development set | • Model gives predictions • Unseen data |

Once the model has been chosen, it is trained on the entire dataset and tested on the unseen test set. These are represented in the figure below:
Ml Cheat Sheet Scikit
Cross-validation Cross-validation, also noted CV, is a method that is used to select a model that does not rely too much on the initial training set. The different types are summed up in the table below:
| k-fold | Leave-p-out |
| • Training on $k-1$ folds and assessment on the remaining one • Generally $k=5$ or $10$ | • Training on $n-p$ observations and assessment on the $p$ remaining ones • Case $p=1$ is called leave-one-out |
The most commonly used method is called $k$-fold cross-validation and splits the training data into $k$ folds to validate the model on one fold while training the model on the $k-1$ other folds, all of this $k$ times. The error is then averaged over the $k$ folds and is named cross-validation error.
Regularization The regularization procedure aims at avoiding the model to overfit the data and thus deals with high variance issues. The following table sums up the different types of commonly used regularization techniques:
| LASSO | Ridge | Elastic Net |
| • Shrinks coefficients to 0 • Good for variable selection | Makes coefficients smaller | Tradeoff between variable selection and small coefficients |
| $...+lambda||theta||_1$ $lambdainmathbb{R}$ | $...+lambda||theta||_2^2$ $lambdainmathbb{R}$ | $...+lambdaBig[(1-alpha)||theta||_1+alpha||theta||_2^2Big]$ $lambdainmathbb{R},alphain[0,1]$ |
Diagnostics
Bias The bias of a model is the difference between the expected prediction and the correct model that we try to predict for given data points.
Variance The variance of a model is the variability of the model prediction for given data points.
Bias/variance tradeoff The simpler the model, the higher the bias, and the more complex the model, the higher the variance.
| Underfitting | Just right | Overfitting | |
| Symptoms | • High training error • Training error close to test error • High bias | • Training error slightly lower than test error | • Very low training error • Training error much lower than test error • High variance |
| Regression illustration | |||
| Classification illustration | |||
| Deep learning illustration | |||
| Possible remedies | • Complexify model • Add more features • Train longer | • Perform regularization • Get more data |
Error analysis Error analysis is analyzing the root cause of the difference in performance between the current and the perfect models.
Ablative analysis Ablative analysis is analyzing the root cause of the difference in performance between the current and the baseline models.
